A Little Something for Teachers 5

The Versatile Number Line

                                                       

One and one is two

Two and two is four

Subtraction and division is less

Addition and multiplication means more.

A fraction is a piece

A decimal fraction is a part

A percentile fraction is not all

So whole numbers is the place to start.

Start with a simple number line

Between each two numbers a space

Starting at the number zero

Up to twelve you may trace.

Twelve is a remarkable number

So much can be done with it

With its factors and facts galore

Make studying twelve a habit.

 

Six numbers can divide twelve

And nothing will be left over

One, itself, two, three, four and six

What an interesting small number!

Explore it on the number line

And compile its interesting stats

Have fun leaping forward and back

And then memorise these facts.

The number line is an aid

From which we can learn much Math

When we learn to use it properly

It takes us to the top of the class.

Examine the number line

Study its numbers and spaces

Learn mathematics from its source

And watch the smiling faces.

What a versatile teaching aid!

Not only whole numbers does it teach

But if we explore its many spaces

The fractions we will also reach.

  

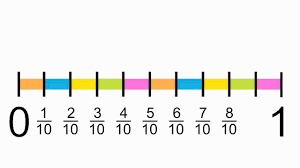
In each space there are halves

And quarters, fourths and fifths

And in that single space

There is an infinite fraction list.

Not only whole numbers and fractions

You’ll find on the number line

Mixed numbers are also there

You can find them anytime.

With a leap beginning at zero

Reach the space between five and six

Find five and a half and five and a quarter

And many more numbers of that mix.

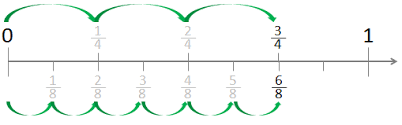
Besides the unit fractions

Of one-half, one-quarter and one-third

We can create two-thirds and three-quarters

Try it out; don’t just take my word.

And if we magnify one of these spaces

Up to one hundred spaces or so

There are decimal fractions and percent

On the number line there is so much we can know.

On the number line we can add

On the number line we can subtract

On it we can divide and multiply

And calculate multiples and facts.

It can be used to learn algebra

It is used to measure our shapes

It is the basis for fitting exactly

Take a look at the measuring tape.

It can be seen on a grid

It is clearly shown on a graph

It is crucial to problem solving

In learning mathematics it’s the path. 

Yet some consider it ancient

And not relevant for today

But it’s a simple remarkable instrument

If we use it in the proper way.

So adopt the number line

And adapt it to each grade

As you explore its versatility

You’ll find it’s a remarkable teaching aid.

I trust these verses of poetry

Would be an advert at this time

As the alphabet is to language

To mathematics it’s the number line.

Stewart Russell © 2016

The Flexible Rule

Somewhat like the number line

Is the rule or the measuring stick,

Once we used the Imperial rule

But these days it is mostly metric.

It is made of wood in some cases

But many are also made of plastic,

Not as popular is the metal rule

But any of them will do the trick.

Do not use as percussion sticks

Or to make music on your desks,

A damaged rule that cannot measure

Is nothing more than useless.

The rule is an important member

It should be in the mathematics pack,

A schoolbag without the essential rule

Is travelling down the wrong track.

Do not use it to introduce measurement

Bring it further down the line,

For measuring without a true concept

Is most difficult to refine.

Start with paces and hand spans

Measure the desks and the floor,

Then move outside to the corridor

And the playing field

If you need to measure more.

Then you will see the need for a rule

With the varying paces and hand spans,

For students come in different sizes

And also their paces and hands.

Use the rule to measure the paces

Use the rule to measure the spans,

Then create a problem in mathematics

And see if the pupils can make a plan.

It would be quite tedious

Measuring the corridor with a rule,

But to find the size of my pace

The rule would be an important tool.

For now knowing the size of my span

And knowing the measure of my pace

I can calculate using the rule

The measure of almost any place.

I can obtain a ball of string

And then wrap it around a tree,

To learn the measure of its diameter

The rule would come in quite handy.

Use the rule to measure the string

It is the same measure as the tree,

And knowing the measure of the string

Will be the diameter’s measure exactly.

A procedure to bear in mind

The rule comes after the number line,

Both show the zero coming first

In measuring remember that every time.

It’s different from counting items

Where the first item is number one,

On the rule there are spaces

Like the paces used to measure the lawn.

I trust the foregoing fourteen verses

Have shown the importance of the rule,

Notwithstanding its shape and rigidity

It can be a flexible measuring tool.

Stewart Russell © 2016 





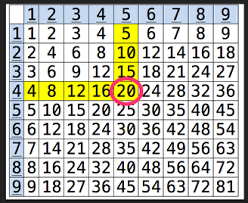
The Multifaceted Grid

You have had the versatile number line

And you have had the flexible rule,

Let us not forget, however,

There is another marvellous tool.

And what is particularly interesting

Is the way the three are linked

For when we include the grid

We see how beautifully they sync.

 

Yes, the multifaceted grid is next

On the list of mathematical tools;

It can be made up with a number line

Or perhaps a measurements rule. 

On the vertical axis could be the rule

With one on the horizontal as well,

And a simple maneuver across and down

One would its area tell.

  

Or perhaps it could be a grid

With multiples of numbers from one to five

Showing common multiples and fractions

Making mathematics come alive.

We would also be able to ascertain

A list of consecutive squares

As we proceed along the diagonal

Of those squares we would be aware.

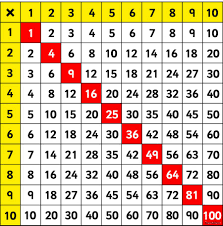
Can’t you see that number grid

Starting with the smallest square?

The square of one then two and three?

Yes! One, four and nine would soon appear.

Next would come sixteen and twenty-five

Then thirty-six and forty-nine

And if we extend the size of that grid

Many more squares we would find.

Or equivalent fractions we should see

As the multiples increase or decrease;

One-third would be equal to three-ninths

As the multiples proceed from the least.

Reduction of fractions would be clear

Just take the opposite direction,

Four-eighths, two-fourths and one-half

Already you should be having fun.

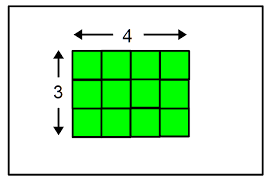
Multiplication would make more sense

As we examine the area model

And division too would fall into line,

The grid would simplify that puzzle.

On the grid you should see the interaction

Between multiplication and division;

Here there is a wonderful attraction

As we process each operation.

One to four along the vertical

And one to three along the horizontal

Produces twelve squares in the area

And there we have our rectangle.

 

Hence we have a beautiful interplay

Between multiplication and division

Right there on our grid

I trust I have your attention.

One basic thing to keep in mind

When operating division on the grid

The vertical is always the divisor

Never the quotient, math forbids.

So much mathematics on the grid

Hence its multifaceted appeal

And once the teachers take the time

So much on that grid can be revealed.

  

As I bring this poem to an end

At two other aspects I’ll take a look:

There are subtraction and addition,

I know it doesn’t appear so in your book.

But having mastered these operations

It doesn’t matter with which you start,

So subtracting fractions could come at first

And from the old tradition you could depart.

The grid facilitates both operations

When combined with fractions equivalence;

The Least Common Multiple appears

In a subtraction or addition instance.

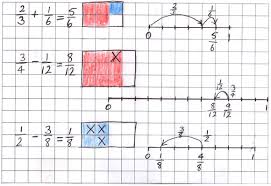
One-half, two-fourths, three-sixths

With one-third and two-sixths compared,

From three-sixths two-sixths I take

And presto!  One-sixth appears.

Whenever we add or subtract

Our terms must be alike

Hence one-half added to one-third

Becomes five-sixths; that’s right!

By now you should have realised

The multifaceted-ness of the grid,

Combined with the rule and number line

For these three how much do you bid?

You've seen the versatile number line

And you have had the flexible rule

Let us not forget, however,

The grid is a multifaceted tool.

Stewart Russell © 2016